Intuitively Teaching About Ferromagnetism/Anti-Ferromagnetism

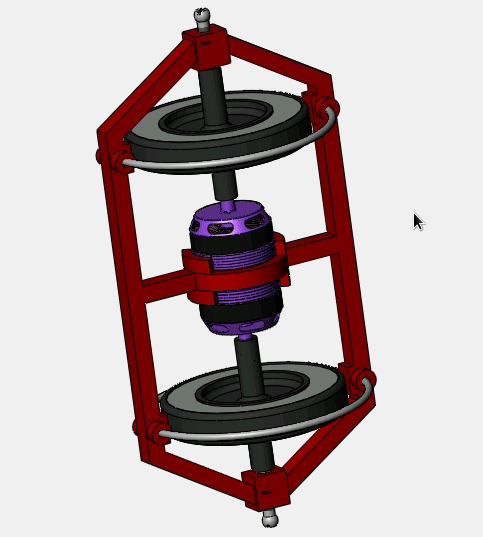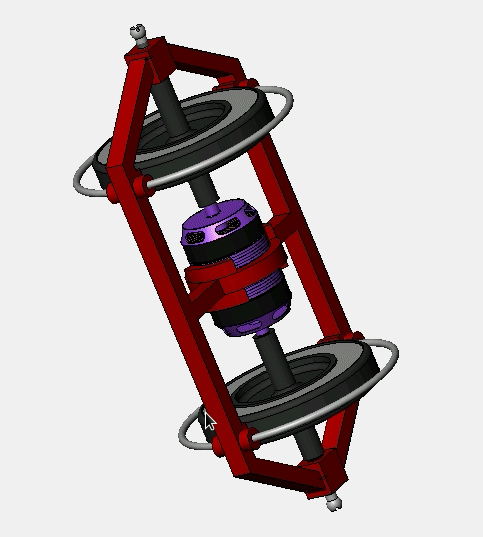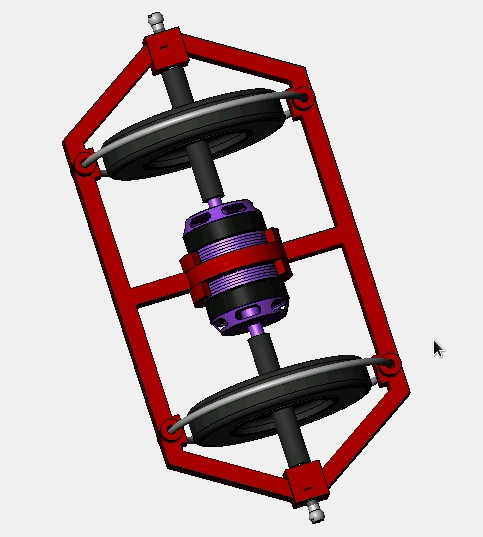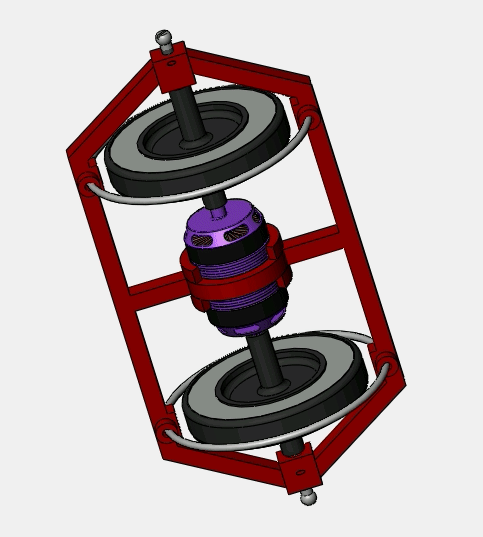
This post & work is still in progress.

Last year, I was given a job to create a toy for general audience for the FU Berlin section of the event ‘Lange Nacht der Wissenschaften’. The toy needs to show intuitively how ferromagnetism and antiferromagnetism works. To put it simply, the spin of electrons needs to align with each other to create magnetism in ferromagnetic materials. Antiferromagnetism is also when the spin of electrons is regularly aligned but with a catch; neighboring electrons now have opposite spins, thus creating a net-zero magnetic field but still ordered magnetism.

The best way to visualize and play out with the idea of electron spin is a spinning top or a gyroscope. Even though one needs to be careful about how far the analogy will hold, still with caution, there is no better way to ‘feel’ the spin other than a mechanical analogy. So with one spinning top, we can have a single electron let’s say. To achieve ferromagnetic/anti-ferromagnetic behavior, we need at least two electrons or spinning tops. So a toy that doubles the gyroscope can playout well. If the person rotates both gyroscopes in the same direction, inertia related to angular momentum will be strongly felt; an analogy of ferromagnetism. If they are rotated to the opposite direction (even though there is same energy in the system as before) the inertia will be pretty small to be felt; an analogy of antiferromagnetism.

So to create this toy, we can already start with the existing ones. Now, the question is, do we want the audience to use a piece of rope or a similar mechanism to be spin the gyroscope? Obviously no, as it will probably be tough to spin both of the tops at similar speeds. So we need electrical motors, but which kind? How much torque and power is required to spin the top?

To calculate this, we need the moment of inertia of our spin-top. The mass of the spin-top is around 106 gr. If we neglect the driving shaft, it is approximately 100gr.

$ I_{zz} = 58301.33 gr (mm^2) \approx 50086.13 gr (mm^2) $ is the moment of inertia for the spin-top. In SI unit, the moment of inertia of a disc is $I= \frac{1}{2}MR^2 = \frac{1}{2}(0.1 kg)(0.0317 m)^2 = 50.25 x 10^{-6} kgm^2$

To find out how much force the spin-top needs to align perpendicular to the normal incidence of the surface, we can calculate the angular frequency in which the precession of the spinning top is minimum. Of course, in the user’s hands, calculating minimum precession regarding gravity doesn’t make sense. Still, otherwise, we need to consider different muscle strengths of people, and I am not sure how to do it even. So, as a common standard, we thought defying gravity is already a pretty good sign of torque.

where $r= 23.15 + 20 \pm 0.06 mm \approx 0.0432 $. 0.06 is uncertainty related to center of mass, 20 is the skeleton length.

$\omega = \frac{mgr}{I\omega}$ -> formula derived for precession angular velocity as a function of $m, r, I $ and $g = 9.806 m/s^2$

and we measured how much time it takes for one precession revolution for an arbitrary angle to see how much $\omega$ is required to defy gravity.

$ t = 1.25 s \rightarrow 0.8 \frac{turn}{second} \rightarrow 2 \pi x 0.8 = 5.024 rad/s = \omega_p $

We need a motor that at least can provide this number but even much more to make a person feel the inertia is related to angular momentum.

To calculate required torque, one should also know the angular acceralation $\alpha$ as;

$ \tau = I \alpha $ and $ \alpha = \frac{\omega}{t} $

and $\omega$ is angular velocity and calculated as $\frac{2 \pi n}{60}$, as n is RPM, so $\alpha = \frac{\pi n}{30t}$, t is accelaration time in second.

From 0 to 1698 RPM in 10 seconds;

and

thus $ \tau = 89.3 x 10^{-5} Nm $

$ Power(kW) = Torque(Nm) x Speed(RPM)/ 9.5488 $

So we would choose a motor with above specifications. A DPDT switch to change rotation from cw to ccw is needed. Also to control speed is important to achieve different values of RPM. Another requirement is to have a light and small dimensional motor. A brushless DC motor would be ideal.

will continue